Séminaire des Doctorants
Séminaire des doctorants du CMAP et du CMLS
Équipe d'organisation : Margherita Castellano, Adrien Majka, Adriano Prade, Shayan Zahedi, Vianney Delasalle, Zoubaïr Tazakkati, Clément Morhain et Adrienne Le Meur.
2025-2026
Mercredi 26 novembre (16h-17h): Quentin Houssier (CMAP)
Introduction to the alignment problem in machine learning.
Training a machine learning model on a task always involves defining a loss function that is supposed to capture what we want the model to do. Although this is sometimes trivial, this step reprensents a real difficulty, particularly because the intentions behind what we ask of the model are sometimes very difficult to translate into a loss function that can be used for optimization, for various reasons (computability, information available at the time of calculation, etc.). We therefore often use a proxy, which imperfectly captuures our real intentions but has the advantage of being easy to use for training: a score in a game, a physical quantity, a statistical approximation, etc. This raises a new question: does training on the proxy, which only partially correlated with our intentions, lead to good results?
Mercredi 26 novembre (16h-17h): Quentin Houssier (CMAP)
A gluey contact model with friction for the numerical simulation of immersed granular media.
Mercredi 12 novembre (16h-17h): Théo Herouard (CMAP)
A (quick) introduction to the mean-field approximation for open quantum systems.
Mercredi 29 octobre (16h-17h): Valentin Pesce (CMAP)
Around random polynomials, towards a continuous-time approach.
This talk will study the following question: given the roots of a polynomial, where are the roots of its derivative located? First, we will review some well-known results concerning the location of the derivative's roots when the initial polynomial's roots are known. In particular, we will emphasise the proof of the Gauss-Lucas theorem and its electrostatic interpretation. Next, we will examine a stochastic problem introduced by Pemantle and Rivin in 2011 that addresses this issue. Suppose the roots of a random high-degree polynomial are independent and identically distributed, where are the roots of its random derivative polynomial located? We will answer this question in certain particular cases as when the roots are real. Finally, we will introduce a heuristic given by Steinerberg in 2018 to have a continuous-time approach to this problem. We shall also mention some notable solutions from classical families of orthogonal polynomials for this PDE approach.
Mercredi 8 octobre (16h-17h): Louis Berthier (CMAP)
Topology-Preserving Learning with Self-Organizing Maps and Applications with torchsom.
Self-Organizing Maps (SOMs), introduced by Teuvo Kohonen in the 1980s, are a class of neural models that combine unsupervised learning with topology-preserving dimensionality reduction. Unlike linear methods such as PCA, SOMs rely on a competitive learning process that maps high-dimensional data into structured low-dimensional representations, most often two-dimensional grids. This property makes them powerful tools for data visualization, clustering, and exploratory analysis, while also offering strong advantages in terms of interpretability, scalability, and applicability in resource-constrained environments. In recent years, SOMs have seen renewed interest as alternatives or complements to popular manifold learning techniques like t-SNE and UMAP, especially in the context of explainable AI and industrial applications.
In this talk, I will first present the foundations of Self-Organizing Maps. Then, I will introduce torchsom, a PyTorch-based library developped to provide a modern, efficient, and extensible framework for SOMs. Compared to existing implementations, torchsom achieves significant gains in computational performance while enhancing objective functions and offering a broad range of diagnostic visualizations and extensions for supervised tasks. I will also highlight some industrial and scientific applications, including our work on online learning strategies for soft sensing in manufacturing.
2024-2025
Mercredi 18 Juin (15h-16h): Nicoleta Cazacu (CMAP)
From Interacting Particle Systems to PDEs: Singular Interactions and Stochastic Approximation of Nonlinear Fokker-Planck Equations.
The derivation of macroscopic evolution equations from microscopic models of interacting particles is a classical problem, tracing back to the pioneering work of Kac on the Boltzmann equation. Since then, extensive research has focused on systems of interacting particles and their convergence to nonlinear Fokker-Planck equations. When interactions are regular (for example Lipschitz continuous) the convergence and associated techniques are now well-understood. However, in the presence of singular interactions, such as those arising from the Keller-Segel, Coulomb or Riesz-derived kernels, many questions remain open, making this an active area of research. In this talk, I will first introduce the framework of moderately interacting particle systems and discuss the concept of propagation of chaos in the singular setting as the number of particles tends to infinity. I will then present recent results and techniques used to obtain convergence results in this singular setting. Finally, I will introduce a stochastic numerical approach—based on the Euler-Maruyama scheme—to approximate solutions of nonlinear Fokker-Planck equations with singular kernels, and discuss its quantitative convergence.
Mercredi 4 Juin (15h-16h): Mahmoud Hegazy (CMAP)
Scalable and Flexible Approaches to Uncertainty Quantification: Utility-Aware Calibration and Conformal Selection.
Model calibration ensures that a classifier's predicted probabilities accurately reflect the true likelihood of outcomes. Conformal prediction provides a framework for creating prediction sets that provably contain the true outcome with a user-specified confidence level, without distributional assumptions. These two approaches are common for uncertainty quantification in machine learning. This exposition provides an overview, then explores concepts from two under-submission works aimed at enhancing the scalability and flexibility of these methods for practical use. Measuring multiclass calibration rigorously is challenging, as common methods often lack scalability or rely on heuristics. To address this, the first work introduces a theoretically-grounded, utility-aware approach. This provides utility-based metrics that refine standard assessments and enable more nuanced, decision-centric analysis, especially with high-dimensional predictors. While conformal prediction offers robust coverage guarantees, a common challenge arises when multiple valid prediction sets exist, as selecting among them typically invalidates these guarantees. The second work presents stability-based methodology to address this. It allows choosing a preferred set (e.g., smallest) from multiple valid options while provably maintaining coverage, thereby enhancing flexibility and adaptability in practical scenarios.
Mercredi 21 Mai (15h-16h): Christoph Schönle (CMAP)
Sampling metastable systems with dimensionality reduction maps.
Sampling from high dimensional multimodal probability distributions is a challenging problem with a wide-range of applications, notably drawing samples from the Boltzmann distribution to describe complex molecules in thermal equilibrium. We consider the special case where a dimensionality reduction map is available that allows for an effective description of the slow (macroscopic) degrees of freedom of the system. Assuming that a good proposal kernel is available in the space of reduced dimensionality, we discuss how one can build an MCMC sampler in the full space to obtain a reversible chain with respect to the target probability measure.
Mercredi 7 Mai (15h-16h): Omri Ben-Dov (Université de Tübingen)
A constrained optimization approach to generative models
Generative models aim to learn and sample from complex, unknown data distributions and have become a central focus of modern machine learning research. In this talk, I will first explain the motivation behind generative modeling and outline the requirements such models should satisfy. I will then provide an intuitive overview of commonly used frameworks, highlighting how they usually face a trade-off that prevents them from fully meeting these requirements. To address this, I will introduce a new perspective that can resolve this trade-off and present supporting results. Finally, I will discuss my current work, which reformulates the generative modeling problem as constrained optimization, and explore its advantages and interpretations.
Mercredi 23 Avril (15h-16h): Mateo Deangeli Bravo (CMAP)
Modeling horizontal gene transfer : scaling-limit and ancestral lineage
This presentation will be an opportunity to introduce some mathematical tools in structured population stochastic modeling, from the example of horizontal gene transfer in bacteria. The main objective is to study the ancestral lineages of the individuals in the population. First, we will present the biological context and recall all the necessary elements of stochastic processes theory, so that everyone can follow. The main object is a measure-valued process, which correctly renormalized by a scaling parameter K, converges (when K goes to infinity) to a (deterministic) density given as the solution of a PDE. In a second step, considering a finite sample of individuals alive in the present, we will study the dynamics of the ancestral lineages, i.e. the process that gives the evolution, backward in time, of a typical lineage of individuals.
Mercredi 9 Avril (15h-16h): Ana Fernández Baranda (CMAP)
Hydrodynamic limit of a stochastic model for hematopoieisis
Hematopoiesis is the process by which blood cells are produced. Until now, the modeling of this phenomenon has assumed a hierarchical structure where, at the moment of differentiation, a cell transitions into a new type of cell. However, recent biological studies suggest that this approach oversimplifies the complexity that hematopoietic cells have, as their phenotypes varies widely and do not allow for a clear separation into distinct categories. This suggests that hematopoiesis is rather a continuous process. In this talk, we will present a discrete jump process with finite number, N, of compartments, where each compartment corresponds to a stage in a cell's maturation. Then, we will discuss the system's dynamics as the number of compartments approaches infinity, representing continuous differentiation as opposed to stepwise differentiation.
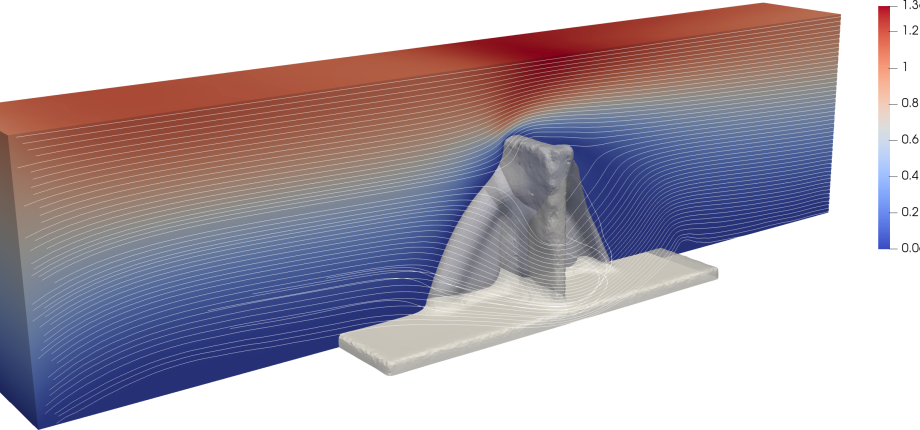
Mercredi 23 Mars (15h-16h): Clément Morhain (CMAP)
How to synthetize turbulence from wavelet decomposition and random cascades ?
The reduced-order simulation (ROS) of turbulent two-phase flows with a dispersed phase (i.e., particles) requires additional modeling to accurately reproduce particle dynamics. ROS involves smoothing the flow, which eliminates small-scale turbulence. However, particle trajectories in turbulent flows are strongly influenced by these small-scale fluctuations. When not explicitly resolved, these fluctuations must be modeled. Two main approaches exist to address this issue. (i) Stochastic models of increasing complexity have been proposed to recover time correlations representative of turbulence along particle trajectories, e.g. intermittency. However, these models fail to reproduce spatial correlations. (ii) Structural models, specifically designed to capture particle segregation (i.e. their concentration in specific regions of the flow), leverage the presence of spatial structures, which can be synthesized using divergence-free wavelets. Nevertheless, they do not include intermittency. Building on divergence-free wavelet decomposition, we aim to integrate stochastic and structural strategies to simultaneously capture both segregation and intermittency. In this context, wavelets and random cascade formalisms complement each other, providing a robust framework for modeling turbulence. Ultimately, the goal is to accurately recover the coupling between particles and the carrier phase.
Mercredi 12 Mars (15h-16h): Giacomo Ceccherini Silberstein (Université de Padoue)
Hamilton Jacobi Equations and Viscosity Solutions in the Space of Probability Measures
Since their introduction by Pierre-Louis Lions and Michael G. Crandall in the early 1980s, viscosity solutions have had a profound impact on the theory of Partial Differential Equations (PDEs), thanks to their wide range of applications. They represent a fundamental concept of weak solutions for a significant class of nonlinear PDEs up to the second order, e.g Hamilton-Jacobi equations (HJEs). In the first-order case, this notion is often motivated by the so-called vanishing viscosity limit, witnessing the stability of this class of solutions under uniform (and smooth, second-order) perturbations. Recently, there has been growing interest in extending the theory and studying nonlinear PDEs in the Wasserstein space, P_2(R^d). In this talk, I will provide a quick overview of the fundamental theory of viscosity solutions in the n-dimensional Euclidean space. Subsequently, I will introduce the HJEs in P_2(R^d) and present, highlighting the challenge of the lack of smoothness of the space, the notion of viscosity solutions to handle both the first-order and "second" order viscous cases. If time permits, I will outline the key ideas—developed in collaboration with my supervisor, Prof. Daniela Tonon—for proving a vanishing viscosity limit with an explicit convergence rate, namely the uniform convergence in P_2(\R^d) of the viscous solutions to the first-order viscosity solution.
Mercredi 26 Février (15h-16h): Lamberto Tresoldi (CMLS)
Weak and Strong Cosmic Censorship Conjectures.
Thanks to Einstein's works of 1905 and 1915, our beliefs about the universe and its structure have changed deeply. Space and time are no longer two absolute and distinct entities, but rather two parts of the same thing, the spacetime. Hence, gravity is no longer interpreted as a newtonian force but as a geometric deformation of the spacetime, induced by interacting bodies. General Relativity is exactly the theory that studies the spacetime evolution, whose dynamics is prescribed by Einstein Field Equations. In this talk we will retrace their derivation as Euler-Lagrange equations and the approach of Choquet-Bruhat and Geroch to prove the well-posedness. Then, we will introduce two of the most central open problems: the Weak and Strong Cosmic Censorship conjectures. In the process of stating the correct formulation given by Christodoulou, we will discuss the concepts of black hole spacetimes, Penrose diagrams, naked singularities and Cauchy horizons.
Mercredi 12 Février (15h-16h): Marta Gentiloni Silveri (CMAP)
Convergence Guarantees for Score-Based Generative Models
Diffusion models are a new class of generative models that revolve around the estimation of the score function associated with a stochastic differential equation. Subsequent to its acquisition, the approximated score function is then harnessed to simulate the corresponding time-reversal process, ultimately enabling the generation of approximate data samples. In this talk, I will address the problem of establishing theoretical guarantees of convergence for diffusion models, that is to say the problem of estimating the distance between the output distribution and the sought data distribution. In order to do so, three sources of error need to be taken into account: the time-discretization error, the score-approximation error and the initialization error. The presentation will be based on two works: KL convergence guarantees for score diffusion models under minimal data assumptions (co-authors: A. Durmus, G. Conforti) and Beyond log-concavity and score regularity: Improved convergence bounds for score-based generative models in w2-distance (co-author: A. Ocello).
Mercredi 29 Janvier (15h-16h): Zoubaïr Tazakkati (CMAP)
Du cinétique au fluide : un modèle aux gyromoments pour le confinement des électrons dans les propulseurs de Hall
Cette présentation sera l’occasion d’introduire les concepts fondamentaux de la modélisation cinétique et fluide, à partir de l’exemple du confinement électronique dans les propulseurs de Hall. Dans un premier temps, nous aborderons la problématique classique du passage de la description cinétique à la description fluide pour un système physique donné. Nous présenterons ainsi l’équation de Boltzmann et les principes permettant d’en déduire les équations macroscopiques classiques de la dynamique des fluides, notamment celles d’Euler et de Navier-Stokes. Dans un second temps, nous étudierons le cas concret du confinement des électrons dans les propulseurs de Hall, mettant ainsi en évidence les défis particuliers posés par ce type de système. En raison de leur complexité, la modélisation de ces systèmes nécessitent en effet une approche spécifique, reposant sur des modèles dits « gyrocinétiques » et conduisant à une classe particulière de modèles fluides : les modèles gyrofluides.
Mercredi 15 Janvier (15h-16h): Maxime Payan (CMAP)
Preuves assistées par ordinateur pour quelque systèmes de réaction diffusion, linéaires et non linéaires
Les équations de réaction diffusion à plusieurs espèces constituent des systèmes avec des difficultés de résolution propres à chacun d'eux. Cependant, grâce à des méthodes assistées par ordinateur, on peut établir des propriétés de ces équations, de manière systématique. Dans un premier temps nous nous intéresserons à un système de diffusion croisée non linéaire et à l'obtention de solution stationnaire à ce système. Une des difficultés principales est la gestion de non linéarités non polynomiales. Après avoir posé un espace de solution adéquat et une “boîte à outils” basée sur les séries de Neumann et les développements de Taylor, nous montrons grâce à un Théorème de Newton-Kantorovitch, l'existence de nombreux états stationnaires. Dans un second temps nous regarderons un système de réaction diffusion linéaire. Nous établirons la stabilité du système relativement à un paramètre libre, en généralisant un théorème de Gershgorin et en utilisant un théorème de Newton-Kantorovitch adapté. Enfin, nous regarderons la question de la stabilité des états stationnaire dans un système de diffusion croisée non linéaire.
Mercredi 11 Decembre (15h-16h): Renaud Gaucher (CMAP)
Nearly optimal breakdown points for Byzantine robust Gossip
Decentralized optimization consists in distributing the computational burden of on optimization problem over multiple computers. The computers have each access to a local function, and they try to collaboratively find a minimizer of the sum of all local functions. This setting has multiple applications, for instance in machine learning where each computer models a datacenter, and the local function corresponds to the performance of a prediction algorithm on this local data. We investigate how to make distributed algorithms robust when some of the computers cannot be trusted and have an adversarial behavior (said « Byzantine failure »). Thus, we mainly focus on the notion of breakdown point, i.e. the number of adversaries an algorithm can tolerate. We show that the maximal breakdown depends on the nature of communication (peer to peer or with a central server). In case of peer-to-peer communications within a communication graphs, we establish links of the breakdown point with eigenvalues of the Laplacian matrix of the graph.
Mercredi 27 Novembre (14h-15h): Loïc Marchesini (CMAP)
The competitive spectral radius of families of nonexpansive mappings
We consider a new class of repeated zero-sum games in which the payoff is the escape rate of a switched dynamical system, where at every stage, the transition is given by a nonexpansive operator depending on the actions of both players. This generalizes to the two-player (and non-linear) case the notion of joint spectral radius of a family of matrices. We show that the value of this game does exist, and we characterize it in terms of an infinite dimensional non-linear eigenproblem. This provides a two-player analogue of Mañe’s lemma from ergodic control. This also extends to the two-player case results of Kohlberg and Neyman (1981), Karlsson (2001), and Vigeral and the second author (2012), concerning the asymptotic behavior of nonexpansive mappings. We discuss two special cases of this game: order preserving and positively homogeneous self-maps of a cone equipped with Funk’s and Thompson’s metrics, and groups of translations.
2023-2024
Mercredi 19 Juin (15h-16h): Leila Bassou (CMAP)
Mean Field Game of Mutual Holding with common noise
We consider the Mean Field Game of Mutual Holding introduced in the paper of Djete & Touzi (2020), within a framework where equity value dynamics are affected by common noise. The problem formulation uncovers a No-Arbitrage (NA) condition that is necessary for the existence of equilibria and streamlines their investigation. The presentation is structured into two parts: The first part is dedicated to the one-period model. We explicitly characterize the NA condition and the mean field equilibria related to a mean-variance criterion. In the second part, we extend the study to a continuous-time setting. Here, we use a weak notion of the NA condition, under which the representative agent's optimization step is reduced to a standard portfolio optimization problem with random endowment. This is a joint work with Mao Fabrice Djete and Nizar Touzi.
Mercredi 4 Juin (15h-16h): Jean Pachebat (CMAP)
Matching Heavy tailed distributions with Generative models: Theory and experiments
Examining extreme events is a critical concern across various fields such as economics, engineering, and life sciences, with wide-ranging applications like ac- tuarial and financial risks, communication network reliability, and aircraft safety. Extreme events play a crucial role also in the context of climate change, with the occurrence of more and more severe weather events, or in the context of cyber- security with the increasing number of cyber-attacks of private companies or public entities. Generative modeling, a Machine Learning framework, aims at reproducing sample from a generative process, may it be from known historical samples (a dataset) or a data density known up to a constant. In this talk, I will present ongoing work on designing Generative Models that match heavy tailed distributions. This work specifically focuses on reproducing the dependence structure in the extremes of a target signal, i.e. regions far from the origin. This presentation will include a theoretical analysis of the problem and illustrations on numerical simulations.
Mercredi 17 mai (15h-16h): Guillaume Broux-Quemerais (LMM, Le Mans Université)
Deep learning scheme for forward utilities using ergodic BSDEs
In this work, we develop a probabilistic numerical method for a class of forward utilities in a stochastic factor model. For this purpose, we use the representation of dynamic utilities using the ergodic Backward Stochastic Differential Equations (eBSDEs) introduced by Liang and Zariphopoulou. We establish a connection between the solution of the ergodic BSDE and the solution of an associated BSDE with random terminal time, defined as the hitting time of the positive recurrent stochastic factor. The viewpoint based on BSDEs with random horizon yields a new characterization of the ergodic cost, which is a part of the solution of the eBSDEs. In particular, for a certain class of eBSDEs with quadratic generator, the Cole-Hopf transformation leads to a semi-explicit representation of the solution as well as a new expression of the ergodic cost. The latter can be estimated with Monte Carlo methods. We also propose two new deep learning numerical schemes for eBSDEs, where the ergodic cost is optimized according either to a global loss function at the random horizon or to the aggregation of local loss functions. Finally, we present numerical results for different examples of eBSDEs and forward utilities together with the associated investment strategies.
Mercredi 24 avril (15h-16h): Orso Forghieri (CMAP)
State Abstraction discovery in Model-Based Reinforcement Learning
In Reinforcement Learning, we embody an agent that evolves within a given environment. At each time step, we take an action and receive a reward along with the next state we visit. In model-based RL, we assume exact knowledge of the state transitions probabilities and subsequent rewards, aiming to determine the optimal policy to maximize the expected sum of future rewards. However, solving the environment model (a Markov Decision Process) suffers from high dimensionality when using traditional dynamic programming method. Hierarchical Reinforcement Learning introduces state and action abstraction as a divide-and-conquer approach on the state and action spaces, mitigating this issue. We focus here on spatial abstraction (division of the state space), maximizing a discounted sum of rewards in an infinite horizon context. As explicit methods for building useful spatial abstractions of models are rare, we present an algorithm that combines Approximate Dynamic Programming with state space disaggregation. Our approach involves aggregations of similar states explaining the underlying MDP structure and ensures convergence to the optimal value. We base our convergence proof on a bound that estimates the quality of any piecewise constant value function approximation based on the related aggregation quality.
Mercredi 10 avril (15h-16h): Armand Gissler (CMAP)
Convergence analysis of evolution strategies with covariance matrix adaptation
In optimization, we seek to identify the global minimum (or maximum) of an objective function. However this task may become difficult, particularly when dealing with nonconvex, multimodal, nondifferentiable functions. I will present evolutionary strategy (ES) algorithms, designed to solve such problems, with a particular focus on ES with covariance matrix adaptation (CMA-ES). Despite empirical evidences suggesting that it converges to the solution of many optimization problems---including highly ill-conditioned problems for which second-order information seems to be learnt---mathematical proofs validating these observations have been lacking. I will present a successful approach to prove convergence of CMA-ES, which relies on the analysis of a normalized stochastic process.
Mercredi 20 mars (15h-16h): Adriano Prade (CMAP)
Fractional Laplacian operator and regularity of nonlocal PDEs
After the breakthrough paper by Caffarelli and Silvestre in 2007, the study of fractional Laplacian and more general nonlocal operators has gained increasing popularity, from both an analytical and a probabilistic point of view. The purpose of the seminar is to present such a class of operators, starting from basic notions and then focusing on the PDEs’ theory developing from them. First, the formula for the square root of the Laplacian (-∆)^½ is provided, together with a few immediate remarks and the motivation behind its name. Then, after introducing the definition of fractional Laplacian (-∆)^s, we give an overview of its main properties, highlighting some similarities and differences with the classical Laplacian (-∆). The second part of the talk is entirely devoted to nonlocal PDEs, reserving particular attention to some regularity issues. We begin by dealing with the possible notions of solutions and next various results available in the literature are outlined. Finally, after introducing the class of Reifenberg flat sets, we present the problem of boundary Hölder regularity of some nonlocal PDEs on this kind of sets, sketching some possible solution strategies if time permits.
Mercredi 6 mars (15h-16h): Jules Delemotte (CMAP)
Evaluating the Skew-Stickiness Ratio in stochastic and rough volatility models
After an introduction to option pricing, we will study the dynamic properties of some classes of stochastic and rough volatility models (including well-known classical examples with their "rough volatility counterpart": the 2-factor Bergomi model, the rough Bergomi model, Heston and rough Heston). For dynamic properties, we intend the dynamics of option implied volatilities, as induced by the model. For some of the recently introduced models (notably rough volatility models), quite some effort in the literature has been concentrated on the analysis of their static properties such as their calibration power or the term structure of ATM skews but, to the best of our knowledge, their dynamic properties have received only little attention so far. One specific indicator of joint spot-price and implied volatility dynamics is the Skew-Stickiness Ratio (SSR), introduced by Bergomi [Bergomi, Smile dynamics IV, Risk 2009] and related to classical smile dynamic regimes (namely, sticky-strike and sticky-delta). We evaluate different estimators of the model SSR -- mainly Monte Carlo based -- and compare the results with the empirical market SSR for some large stock indices, which sheds light on the interest of using a certain modeling choice with respect to another. With a view on explicit approximation formulas, we build on the celebrated Bergomi-Guyon expansion for ATM implied volatilities and skews so to obtain explicit expansions of the model SSR, for which we analyse the accuracy with respect to our Monte Carlo benchmark.
Mercredi 28 février (15h-16h): Charles Meynard (CMAP)
Noise through an additional variable for mean field games master equation on finite state space
This paper provides a mathematical study of the well-posedness of master equation on finite state space involving terms modelling common noise. In this setting, the solution of the master equation depends on an additional variable modelling the value of a stochastic process impacting all players. Using technique from viscosity solutions, we give sufficient conditions for the existence of a Lipschitz continuous solution on any time interval. Under some structural assumptions, we are even able to treat cases in which the dynamics of this stochastic process depend on the state of the game.
Mercredi 14 février (15h-16h): Antoine Van Biesbroeck (CMAP)
Construction de priors de référence en inférence bayésienne, application à l’estimation de courbes de fragilité sismique
Les courbes de fragilité sismique quantifient la probabilité de défaillance d’une structure mécanique conditionnellement à une Mesure d'Intensité (IM) d’un signal sismique. L'estimation des courbes de fragilité s'effectue à partir de données constituées de paires signal sismique (entrée fonctionnelle) et défaillance de la structure (sortie binaire). Les méthodes paramétriques traditionnelles sont souvent mises en défaut en raison du nombre limité de données disponibles dans ce contexte. L’approche bayésienne permet un apprentissage efficace des paramètres d’intérêt, mais reste tributaire du choix du prior, pour lequel toute subjectivité est à proscrire. Nous proposons l’appui de la théorie des priors de référence, que nous enrichissons d’une généralisation de la définition d’information mutuelle, pour justifier l’implémentation du prior de Jeffreys dans notre cadre d’étude. Nos résultats démontrent la supériorité et la robustesse de ce dernier comparé à la littérature, tout en soulignant la sensibilité des estimations au choix du prior et l’impact de la corrélation de l’IM sur la dégénérescence des courbes de fragilité. Nos conclusions mettent en avant l’importance d’une construction objective du prior dans les études bayésiennes.
Mercredi 25 janvier (15h-16h): Emmanouil Sfendourakis (CMAP)
Understanding the worst-kept secret of high-frequency trading
After an introduction to optimal control, we present the stakes of market-making problems and their adaptation to the mechanism of limit order books, which is the way most securities are traded in electronic markets. The volume imbalance is often considered as a reliable indicator for predicting future price movements. In this study, we confirm this statement by analyzing an optimal control problem in which a market maker controls volumes in the limit order book of a large-tick stock and quotes prices at a half-tick distance from the mid-price. We model the mid-price, which is not a controlled variable, using uncertainty zones. The market maker has information about the underlying efficient price and consequently of the probability of a price jump in the future. By using this information , it is optimal for the market maker to create imbalances which are predictive of price movements. The value function of the market maker's control problem can be understood as a family of functions, indexed by the level of the market maker's inventory, solving a coupled system of PDEs. We show existence and uniqueness of smooth solutions for this coupled system of equations. In the case of a continuous inventory, we also prove the uniqueness of the market maker's optimal control policy.
Mercredi 6 décembre (15h-16h): Pierre Mackowiak (CMAP)
Équation de Gross-Pitaevskii avec potentiel bruit blanc
L'équation de Gross-Pitaevskii avec potentiel bruit blanc est une équation de Schrödinger non-linéaire qui comporte un terme de bruit multiplicatif. Elle apparaît comme un modèle jouet dans l'étude des condensats de Bose-Einstein en milieu inhomogène. Je présenterai les résultats que j'ai obtenus en dimension 1 et 2 concernant l'existence et l'unicité de solutions. En dimension 1, le bruit est suffisamment régulier pour obtenir des solutions locales par point fixe. En dimension 2, le bruit est singulier et une procédure de renormalisation est nécessaire pour donner un sens à l'équation. J'expliquerai cette renormalisation, puis je donnerai une idée de la preuve d'existence globale pour les non-linéarités cubiques.
Mercredi 22 novembre (15h-16h): Grégoire Szymanski (CMAP)
The two square root laws of Market Impact and the role of sophisticated market participants
In this study, we revisit the Hawkes order flow model for market impact initially introduced by Jaisson in 2015, which assumes linear market impact for individual orders and a price process modeled as a martingale. Our approach extends this model by introducing sophisticated market participants capable of reshaping the volatility profile. The strength of our methodology lies in two primary aspects: firstly, it relies on minimal or no additional assumptions, and secondly, it yields closed-form expressions for market impact. Notably, our analysis leads to the recovery of two well-known square root laws. Specifically, for a fixed duration, market impact scales proportionally to $\sqrt{\gamma}$, where $\gamma$ denotes the participation rate. Additionally, for a given order size, market impact adheres to a power-law behavior with respect to the total duration.
Mercredi 8 novembre (15h-16h): Roberta Flenghi (CERMICS, Ecole des Ponts)
Central limit theorem for the stratified selection mechanism
The stratified resampling mechanism is one of the resampling schemes commonly used in the resampling steps of particle filters. In the present paper, we prove a central limit theorem for this mechanism under the assumption that the initial positions are independent and identically distributed and the weights proportional to a positive function of the positions such that the image of their common distribution by this function has a non zero component absolutely continuous with respect to the Lebesgue measure. This result relies on the convergence in distribution of the fractional part of partial sums of the normalized weights to some random variable uniformly distributed on [0,1], which is established in a companion paper by overcoming the difficulty raised by the coupling through the normalization. Under the conjecture that a similar convergence in distribution remains valid at the next steps of a particle filter which alternates selections according to the stratified resampling mechanism and mutations according to Markov kernels, we provide an inductive formula for the asymptotic variance of the resampled population after n steps. We perform numerical experiments which support the validity of this formula.
Mercredi 25 octobre (15h-16h): Mohamed Gharafi (CMAP)
Algorithmes mono-objectifs assistés par modèles de substitution pour résoudre des problèmes d'optimisation multi-objectifs
Multiobjective optimization (MO) problems involve balancing multiple, often conflicting objectives, resulting in diverse, incomparable solutions. Solving these problems typically demands costly algorithms due to the challenge of approximating the Pareto set, which may be infinite. Especially when dealing with expensive black-box functions, minimizing function evaluations is crucial.
Sofomore is a framework that leverages existing high-performance single-objective algorithms, such as CMA-ES, to solve MO problem. By construction, It allows easily the extension of single-objective algorithms to costly setups through surrogate-assisted single-objective variants. In this presentation, we propose novel algorithms within the Sofomore framework, tailored for MO problems with expensive functions.
Mercredi 11 octobre (15h-16h): Songbo Wang (CMAP)
Uniform-in-time propagation of chaos for mean field Langevin dynamics
We study the mean field Langevin (MFL) dynamics and the associated $N$-particle system under the functional convexity of the energy. We establish the particle system’s uniform-in-$N$ exponential convergence, and, by combining this with standard finite-time propagation of chaos, we obtain a uniform-in-time propagation of chaos result. If time permits, I will also talk about $L^p$-convergence of MFL and hypocoercive systems.


