EDP Phys

Responsable : Anne de Bouard, Directrice de Recherche CNRS

Membres permanents :

Maxime Breden, Maître de Conférence
Flore Nabet, Maître de Conférence
Roman Novikov, Directeur de Recherche CNRS

Chercheurs associés :

François Alouges, Professeur à l'ENS Paris-Saclay  
Vincent Giovangigli, Directeur de Recherche Emérite CNRS
Ludovic Goudenege, Chargé de Recherche CNRS, CentraleSupelec
Jean-Claude Guillot, Professeur retraité de l’Université Paris XIII
Aline Lefebvre-Lepot, Directrice de Recherche CNRS, ENS Paris-Saclay
Jean-Claude Nédélec, Professeur retraité de l’Université de Rennes

Doctorants, Post-Doctorants :

Margherita Castellano, Doctorante CMAP
Théo Hérouard, Doctorant CMAP
Quentin Houssier, Doctorant CMAP
Pierre Mackowiak, Doctorant CMAP
Maxime Payan, Doctorant CMAP

Stagiaires :

Pei-Cheng Kuo (National Taiwan University)

Activités de recherche:

Les membres de notre équipe étudient des problèmes physiques au moyen de modèles basés sur des EDP principalement non linéaires, du point de vue de la modélisation, de l'analyse mathématique ou numérique, et de la simulation numérique. Nos domaines d'intérêt comprennent la mécanique des fluides, en particulier l'interaction fluide-structure ou les fluides réactifs, l'électromagnétisme et en particulier le ferromagnétisme, la propagation dans les milieux dispersifs (optique non linéaire, atomes froids), les problèmes inverses, l'acoustique.

Mécanique des fluides

Interactions fluide-structure :

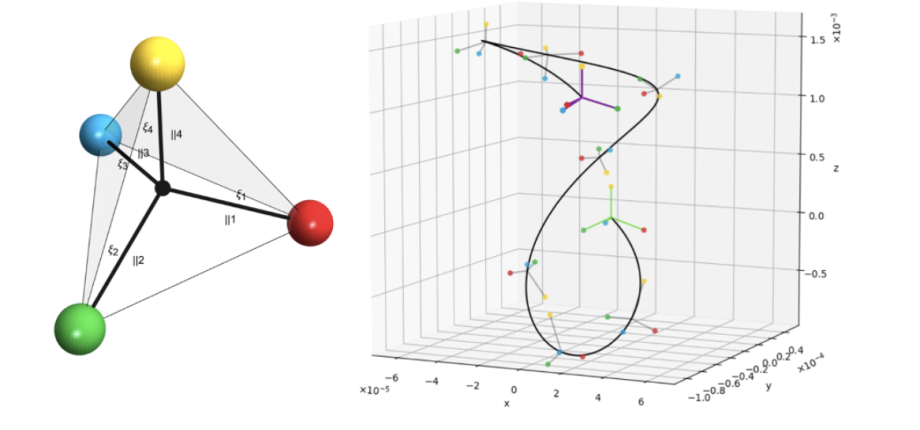
Nous nous intéressons à l’étude de la nage à faible nombre de Reynolds — typiquement celle des micro-organismes — qui s’avère, d’un point de vue théorique, être un problème de contrôle possédant une structure universelle. Nous développons également des stratégies numériques permettant de comprendre la capacité de nage optimale des micro-organismes.

Nous développons des méthodes de simulation de collections de particules en interaction (flot granulaire, suspensions, mouvements de foule) à l’aide du logiciel SCoPi (http://www.cmap.polytechnique.fr/~lefebvre/SCoPI/) pouvant prendre en compte des forces de lubrification, à travers un modèle de contact visqueux.

Fluides réactifs :

Nous nous intéressons à la modélisation, l’analyse mathématique et la simulation numérique d’écoulements réactifs multi-composants, le transport multi-composant dans les mélanges partiellement ionisés en présence de champ magnétique, les fluides réactifs non idéaux, les instabilités hydrodynamiques et la combustion sur-critique.

Equations paraboliques non-linéaires :

Nous nous intéressons à la mise en place et l'analyse de schémas numériques de type volumes finis ou éléments finis pour l'étude de diverses équations paraboliques non-linéaires, possiblement dégénérées. En particulier, on considère modèles d'écoulements en milieu poreux ainsi que des méthodes à interfaces diffuses permettant de modéliser des écoulements diphasiques incompressibles de fluides non-miscibles. Nous considérons également dans ces modèles la présence de fluctuations ou d'onhomogénéités se traduisant par l'introduction de termes stochastiques.
 

Electromagnétisme

Micromagnétisme :

Nous nous intéressons, à la théorie variationnelle introduite par W. Brown pour décrire le comportement des matériaux ferromagnétiques, qui consiste en une perturbation non locale de l’énergie de Dirichlet, soumise à une contrainte non linéaire puisque la longueur de l’aimantation est constante. Nous étudions la gamma-convergence de l’énergie micromagnétique dans certains régimes particuliers, ainsi que la déstabilisation de l'aimantation (phénomène de nucléation). Nous nous intéressons également à la construction de schémas numériques pour la résolution des équations de Landau-Lifshitz, mais également à l'homogénéisation de ces équations.

Problèmes inverses :

Nous nous intéressons à la théorie mathématique des problèmes inverses consistant à déterminer la structure d’un objet à partir de ses données spectrales, problèmes possédant de nombreuses applications, notamment dans le domaine de l’imagerie médicale. Nous élaborons en particulier des méthodes de résolution de problèmes inverses multidimensionnels, possédant des applications pratiques, et nous les justifions mathématiquement.

Ondes non linéaires dispersives :

Nous nous intéressons à la modélisation de la propagation de la lumière dans les fibres optiques, en particulier en présence d’inhomogénéités. Les modèles décrivent l’enveloppe du champ électrique et sont basés sur des équations de Schrödinger non linéaires stochastiques, les fluctuations pouvant affecter la dispersion ou se traduire par des phénomènes de biréfringence aléatoire. Par ailleurs, nous étudions la convergence du système de Zakharov (modélisant les ondes des Langmuir dans un plasma partiellement ionisé) en présence de bruit, vers une équation de Schrödinger non linéaire stochastique.

Preuves assistées par ordinateurs

Nous développons des techniques de "validation a posteriori", qui permettent de démontrer l'existence d'une solution à un système d'EDO ou d'EDP dans un petit voisinage (explicite) d'une solution approchée calculée numériquement. L'intérêt de ces techniques est double. D'une part, elles produisent des estimations d'erreur a posteriori qui sont complètement calculables et garanties (même les potentielles erreurs d'arrondi sont prises en compte). D'autre part, elles peuvent permettre d'obtenir des résultats d'existence dans des contextes où les techniques classiques d'analyse des équations non-linéaires ne s'appliquent pas (par exemple des systèmes avec une dynamique complexe, où de multiples états d'équilibres co-existent, sans paramètre arbitrairement petit ou grand qui pourrait simplifier l'analyse).  Nous cherchons notamment à établir un cadre théorique pour appliquer ces techniques à des EDP paraboliques et des équations stochastiques, avec en particulier des applications en dynamique des populations (systèmes de diffusion croisée) et en mécanique des fluides (équations de Navier-Stokes).

Théorie quantique des champs

Nous étudions la théorie spectrale de modèles issus du Modèle Standard pour les particules élémentaires faisant intervenir les interactions faibles des leptons, des neutrinos et des bosons intermédiaires.